안경쓴 코린이

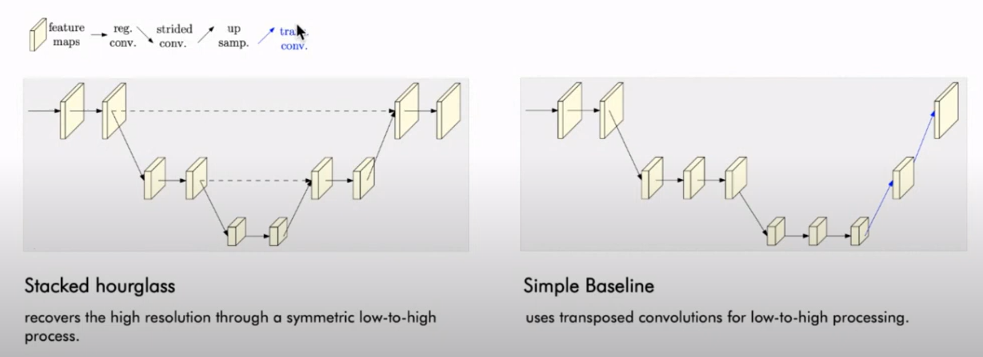
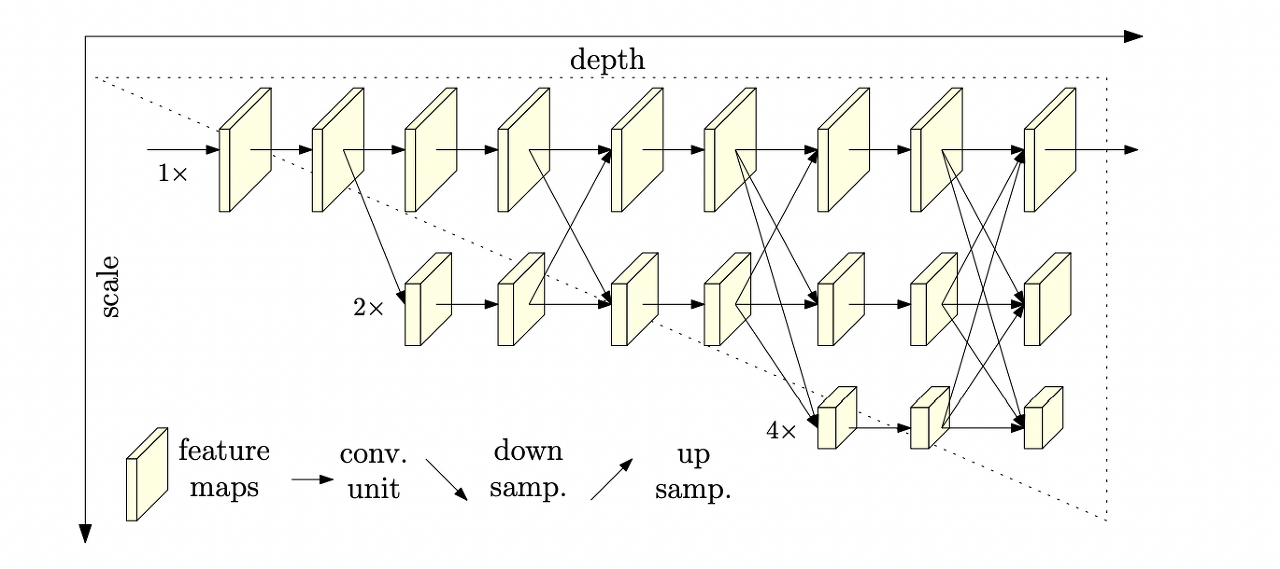
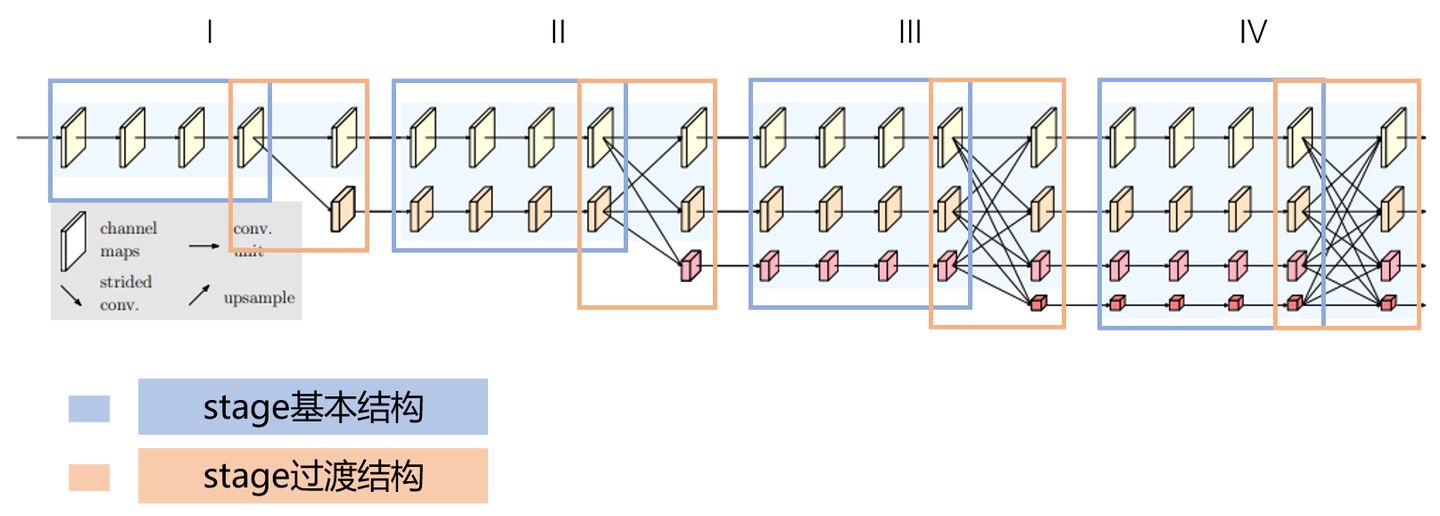
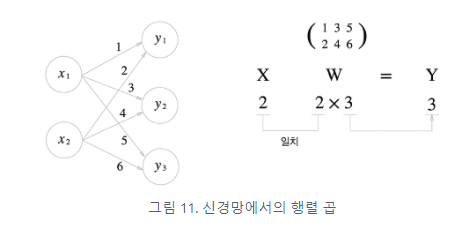
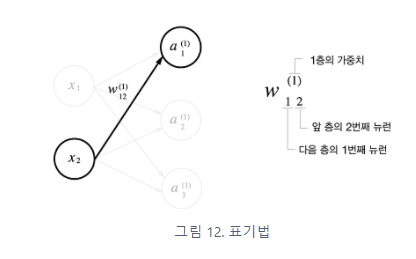
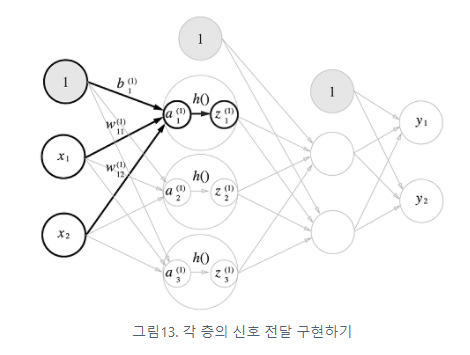
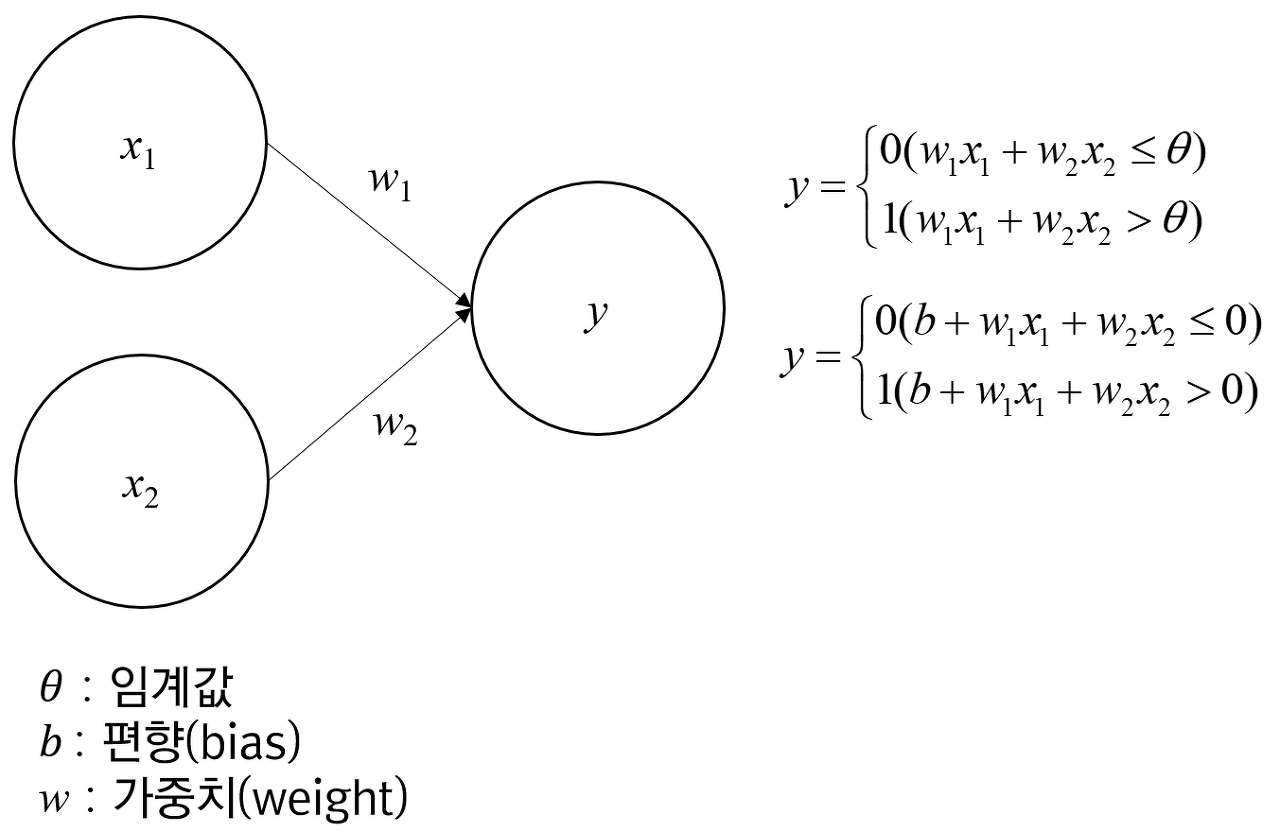
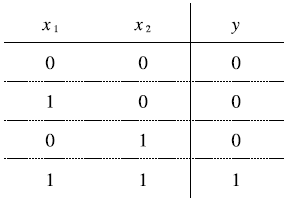
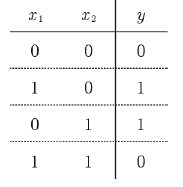
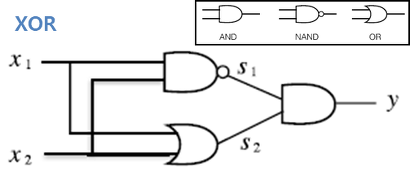
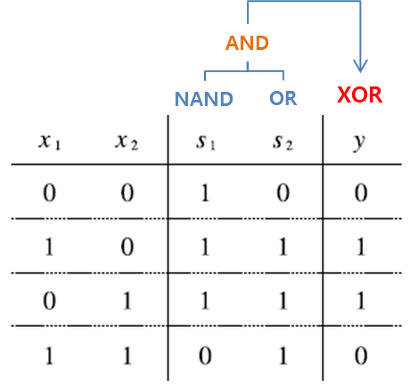
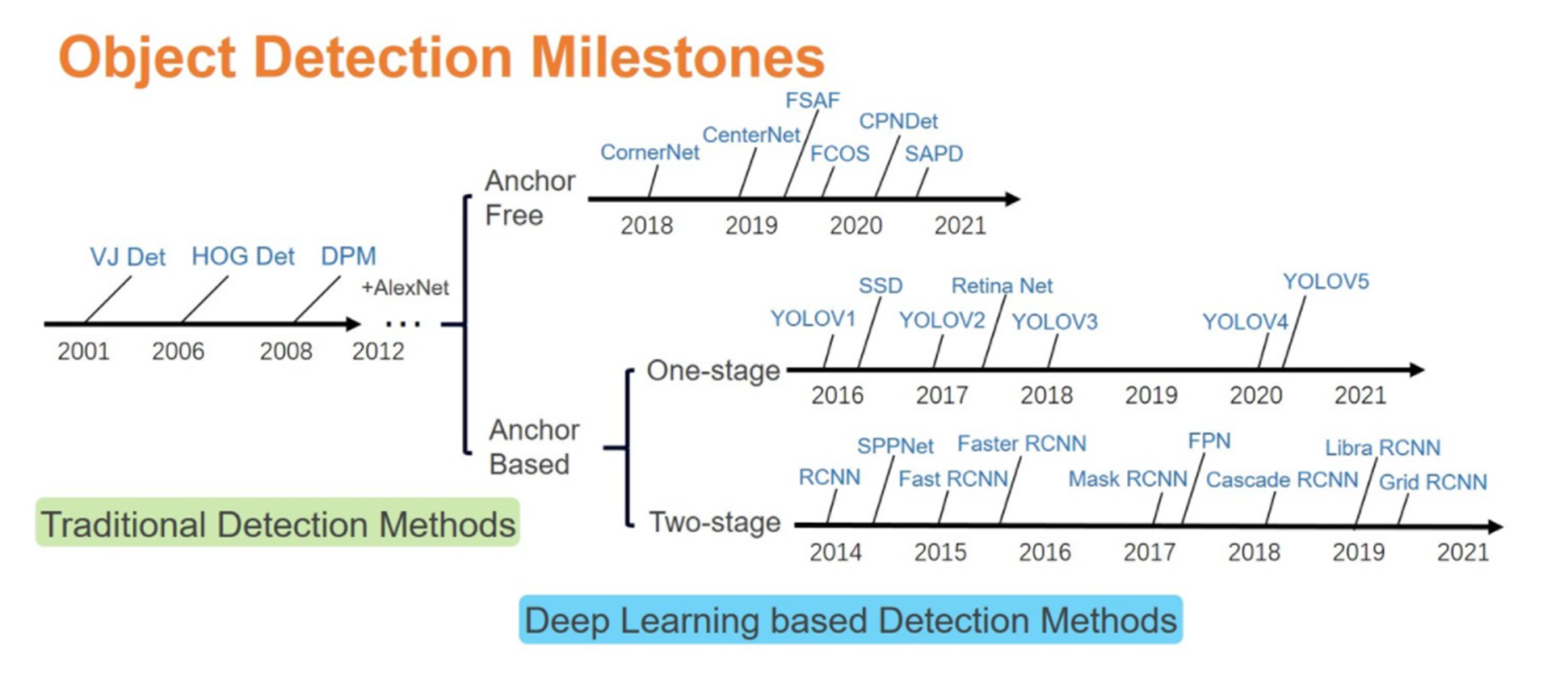
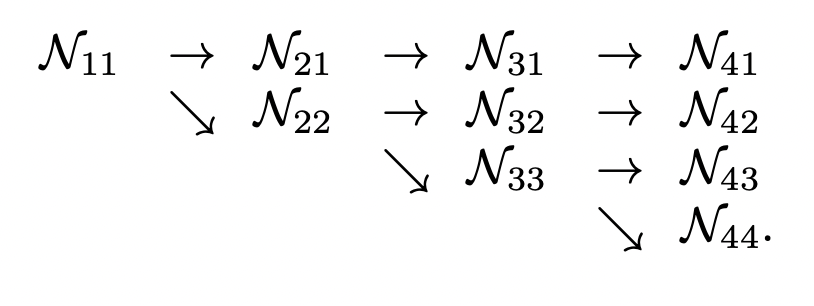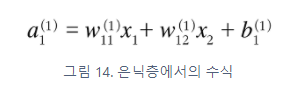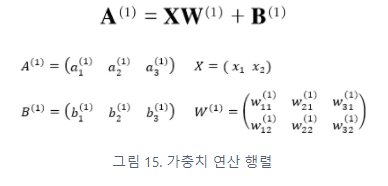anchor based 방식의 흐름

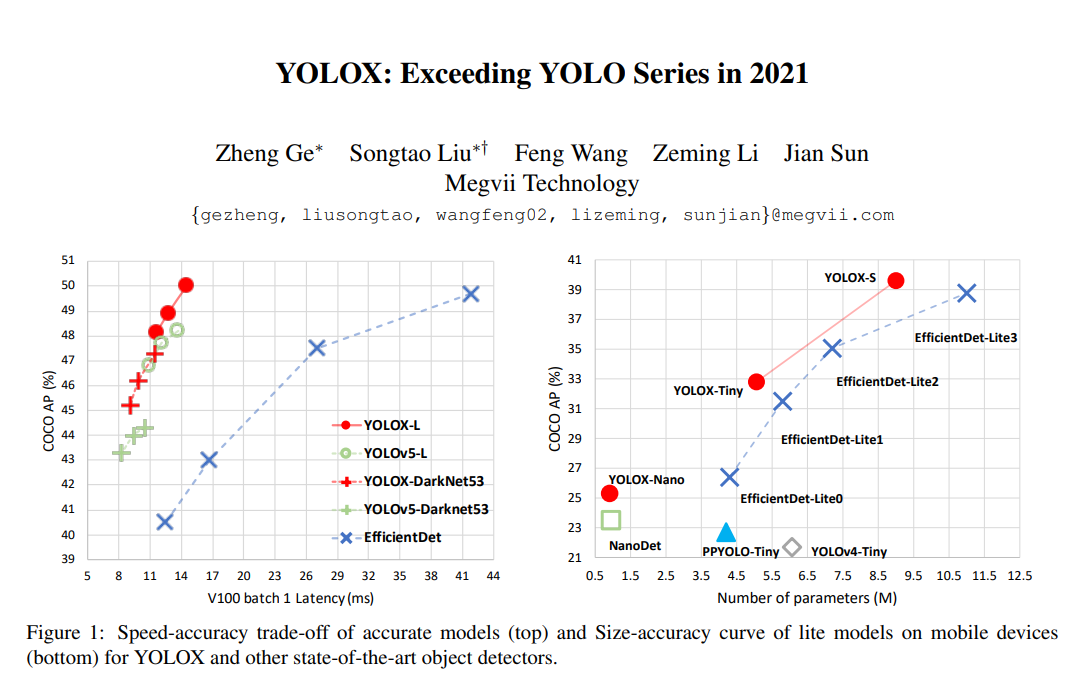
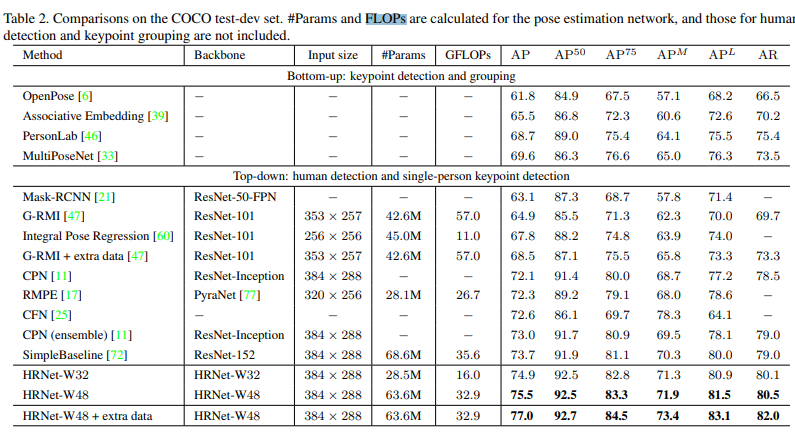
왼쪽 그래프의 성능을 보게 되면 SOTA 모델인 EfficientDet 모델보다 성능이 월등히 높게 나온것을 알 수 있습니다.

(먼저 간단하게 YOLO의 역사에 대해서 언급하고 시작하겠습니다.)

2개의 branch로 나눈 다음에

1. Introduction / brief history of YOLO

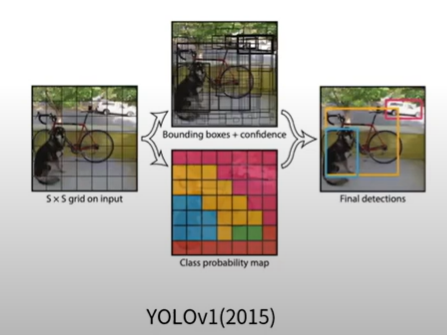
- YOLO(You Only Look Once)는 이미지 전체를 한번에 처리하는 Object Detection의 대표적인 1-Stage Approach
- Real-time Object Detection으로 큰 주목
- 그 후 해를 거듭하며 발전 ( YOLOv1, v2, v3, v4, v5, PP-YOLO, ... )
- 최근에 트랜스포머 계열의 모델들이 Object Detection 태스크에 들어오기 전에는 대부분의 Object Detection 모델들은 CNN개반으로 수행했는데, 이번에 다루는 YOLO 역시 대표적인 CNN 기반의 네트워크 

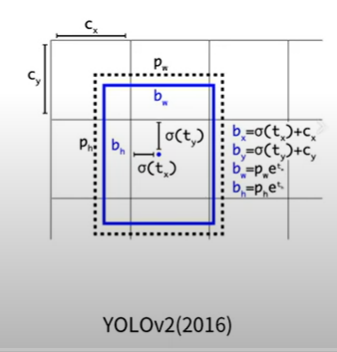
해당 모델이 어떻게 발전했는지를 간단하게만 소개해 드리자면,

1. Introduction / YOLOX Overview

- 최근 2년동안 연구자들은 Anchor-Free Detector, Advanced Label Assignment Strategy, End-to-end Detector의 연구에 주목하였지만 YOLO 시리즈에는 적용되지 않음
- 따라서 본 논문에서는 그러한 좋은 기법들을 적용하여 성능 개선에 목적을 두었다.

• Key concepts
  1. Anchor-free 방식의 Yolo구조
  2. Object Detection을 위한 발전 기술 적용 :
     • Decoupled head ( head를 분리 )
     • 발전된 Label assignment 기법 적용 : SimOTA
     • 강력한 data augmentation : Mosaic, Mixup
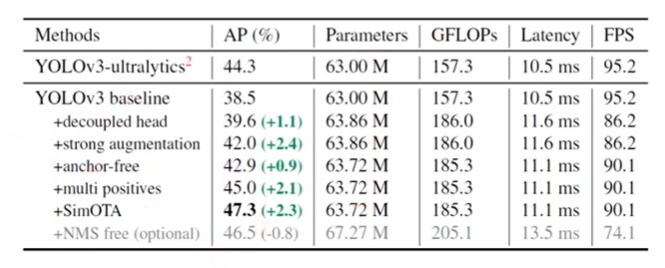
• YOLOv3 baseline
  • YOLOv4, v5가 anchor-based 파이프라인에 과도하게 최적화 될 수 있음을 고려하여 YOLOv3-SPP를 base architecture로 선정

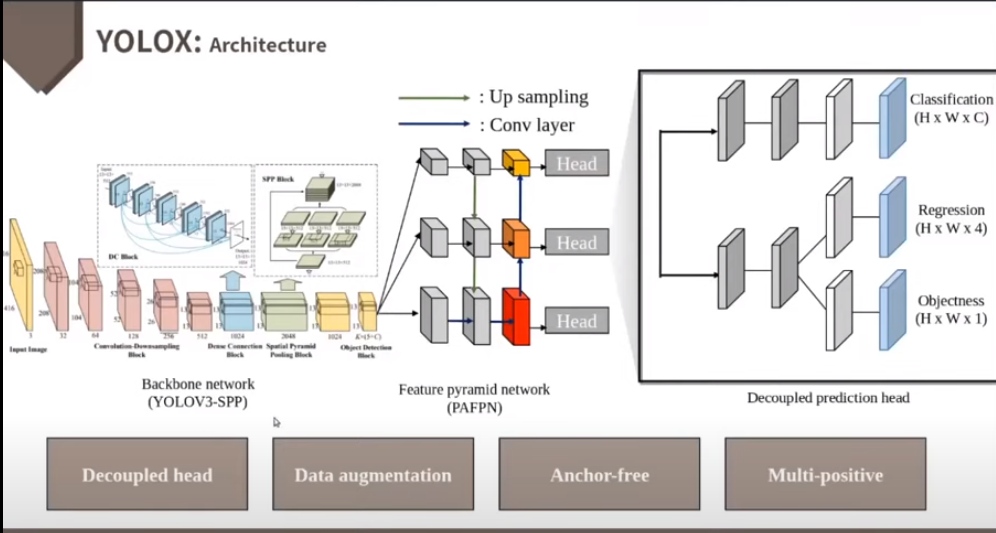
2. Network Design / Architecture

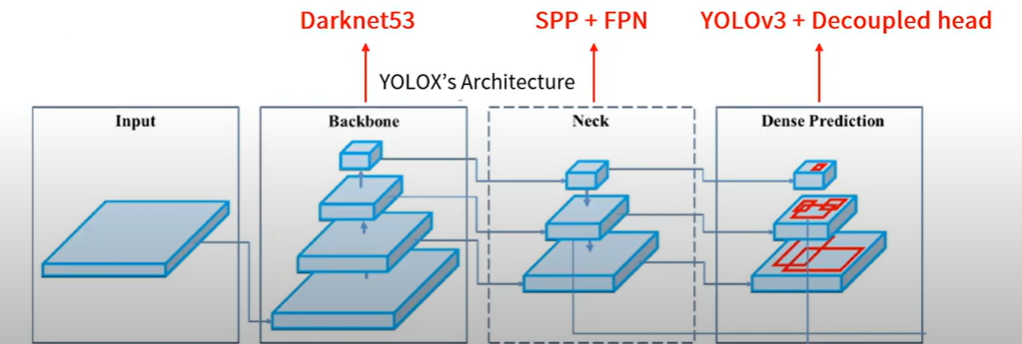
• Architecture
  • Backbone : Darknet53
  • Neck :SPP(Spatial Pyramid Pooling) + FPN(Feature Puramid Network)
  • Head : YOLOv3 + Decoupled head

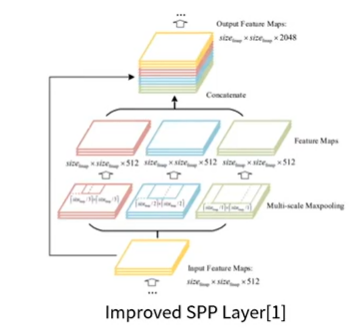
해당 관련 논문 : https://arxiv.org/abs/1903.08589 참고 바랍니다.

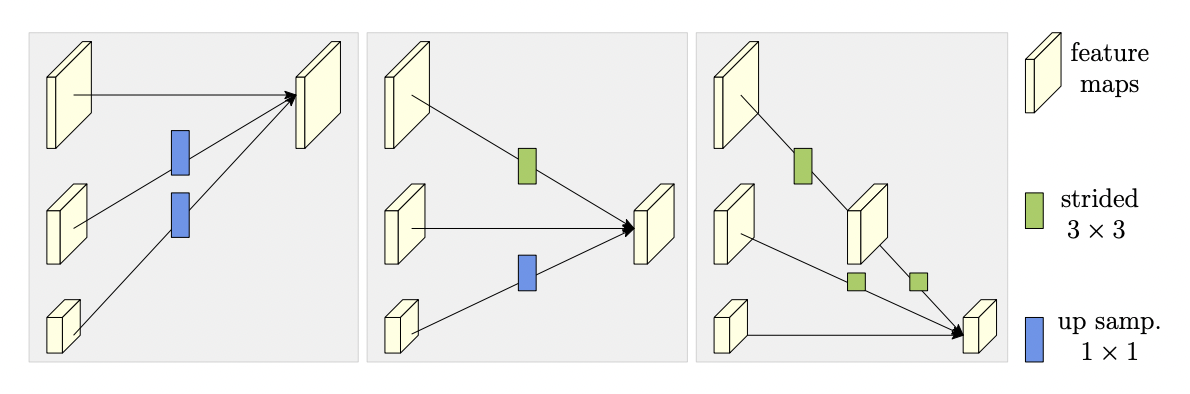
- 먼저 Backbone인 DarkNet에서 feature map을 추출합니다.
- Neck에서는 위에 그림과 같이 공간구조의 정보를 유지는 SPP Layer를 사용합니다. ( 이와 관련된 내용은 추후 추가적으로 다룰 예정)
- 그리고 FPN을 통해 멀티 스케일 Feature map을 얻을 수 있습니다.
- Feature에 대한 성숙도가 낮은 아래의 Feature map의 문제를 개선할 수 있는데요.  high level의 extraction 정보를 더함으로써 아래의 Feature map이 지니고 있는 위치정보를 같이 활용할 수 있습니다.
- Dense Prediction을 보게 되면 위에서부터 큰 물체, 중간 물체, 작은 물체 순으로 detection하는 feature map

2. Network Design / Anchor-free

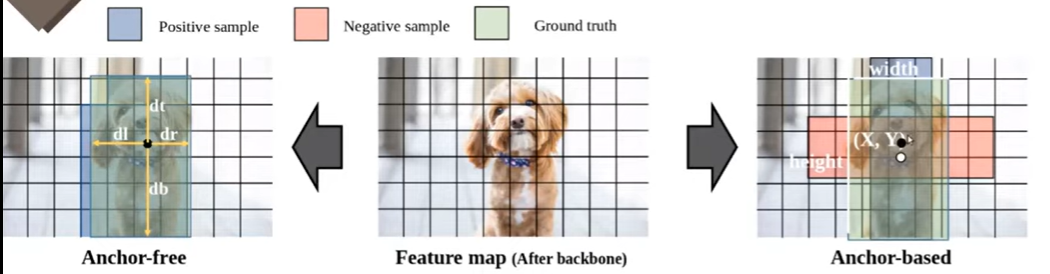
가운데 그림이 Backbon network를 거친 최종 피쳐맵을 의미합니다,
좌측의 경우 Anchor-free 우측의 경우가 Anchor-based 방법을 나타내고 있습니다.

Anchor-based

위의 그림을 보게 되시면 검은 점에서 prediction을 진행한다고 가정을 했을 때, 해당 Cell에서 Regression을 진행 후 나온 output값을 바탕으로 Anchor의 중심점과 가로와 세로의 길이를 결과적으로 bounding box의 가로 세로 길이와 중심점을 학습한다고 보시면 됩니다. ( 이는 네트워크마다 조금씩 다를 순 있습니다.) 여기서 예시를 보게 되면 하나의 Anchor box가 빨간색 박스와 파란색 박스를 만들었다는 걸 의미합니다. 여기서는 초로색 GT box와 초록색 box의 iou값이 높기 때문에 파란색 bounding box가 Positive 샘플로 분류가 됩니다. 빨간색 box는 학습에 참여하지 않음

Anchor-free

위와는 조금 다르게 Anchor-free에서는 GT box안에 있는 Cell들이 전부 Positive 샘플이 됩니다. 예를 들어 위에 그림과 같이 검은 점에서 prediction을 진행 한다고 했을 때, 해당 Cell에서부터 Ground Truth의 각 모서리까지의 길이를 학습하게 됩니다. 이를 바탕으로 Detectiion Task를 수행하게 됩니다.

• Anchor-based design의 단점
  • 도메인에 specific해서 다른 데이터에 generalization 어려움 ( 최적의 anchor box 배치가 그 도매인에 specific하게 만듬 ) - ex) 데이터 셋에 따라서 aspect ratio 비율이 달라질 수 있음
  • head의 복잡성과 예측의 수를 증가
• FCOS 방식의 Anchor-free design 적용
  • FCOS[1]는 anchor-based detector의 단점을 개선한 anchor-free detector
  • Bounding box regression의 범위를 feature level에 따라 pre-define
  • 같은 위치에서 여러 개의 bounding box detect 가능

위의 그림을 추가적으로 설명하자면 YOLOX에서는 같은 포인트에서 두개의 Bounding box를 예측할 수 있는데, 그 이유는 낮은 feature level에서 하나만 예측하도록 ranage를 제한. 즉, feature level에 따라 range가 pre-define

2. Network Design / Architecture

• Object detection에서 Classification과 Regression이 서로 상충하는 문제가 존재함[1](아래 논문 참고)
  • 링크 : https://arxiv.org/abs/1904.06493 

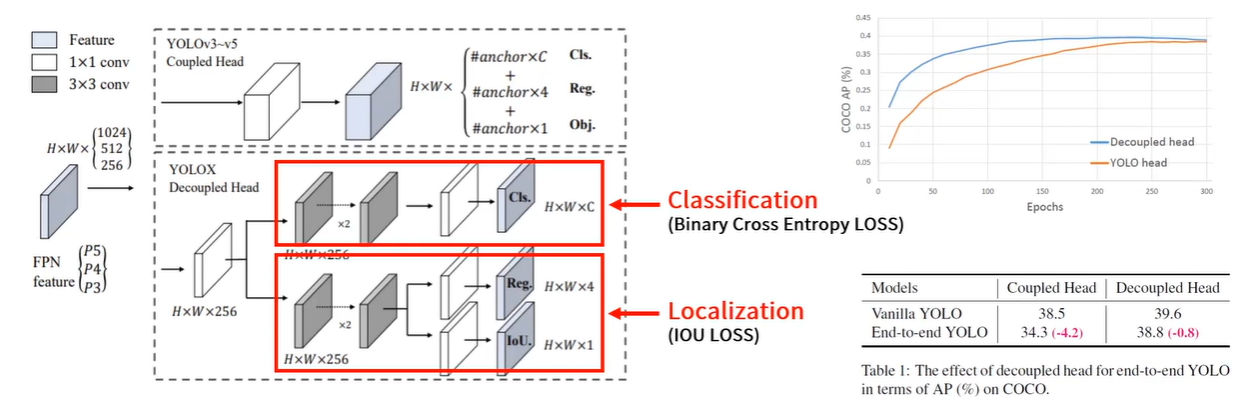
• Head를 Classification과 Regression으로 분리하고 IoU를 추가
  • feature map의 결과를 256 Channel로 줄이고  3x3 Conv를 지나는 2개의 branch를 추가
  • Classification에는 Binary Cross Entropy Loss를 사용해서 각각의 clss에 대한 확률이 나옴
  • Localization에서는 IOU Loss를 사용하여 Bounding Box에 대한 종횡거리가 나오게 됨
    • Loclization의 경우 Regression과 Objectness를 포함
      • Regression Bounding Box에 대한 종횡거리
      • Objectness의 경우 해당 cell이 백그라운드를 나타내는지 아니면 어떠한 오브젝트라도 포함하는지를 0~1사의 value로 표현
• YOLOv3~v5에서 1개였던 기존 head를 분리하면서 수렴 속도와 end-to-end의 AP를 항샹시킴

3. Training Strategies / Strong data augmentation

저자는 여기서 총 4가지의 Data augmentation의 방법을 적용하였습니다.
1. Random horizon flip
2. Color jitter ( 원본 영상의 hsl을 변경하여 증강시키는 클러스터라는 방법 )
3. Mosaic ( 원본 이미지외에 3개의 추가적인 사진을 섞는 방법 )
4. Mixup ( 이미지랑 레이블에 다른 거를 조금씩 섞는 방법 )
( 강력한 Data aumentation을 사용해서 그런지 몰라도 pre-trained weight를 사용해도 성능향상이 별로 일어나지 않아서 scratch 학습을 진행했다고 하는데 일반적인 데이터 셋인 코코 데이터 셋에서 이러한 현상이 발견된 점은 신기합니다. )

3. Training Strategies / Multi-positive

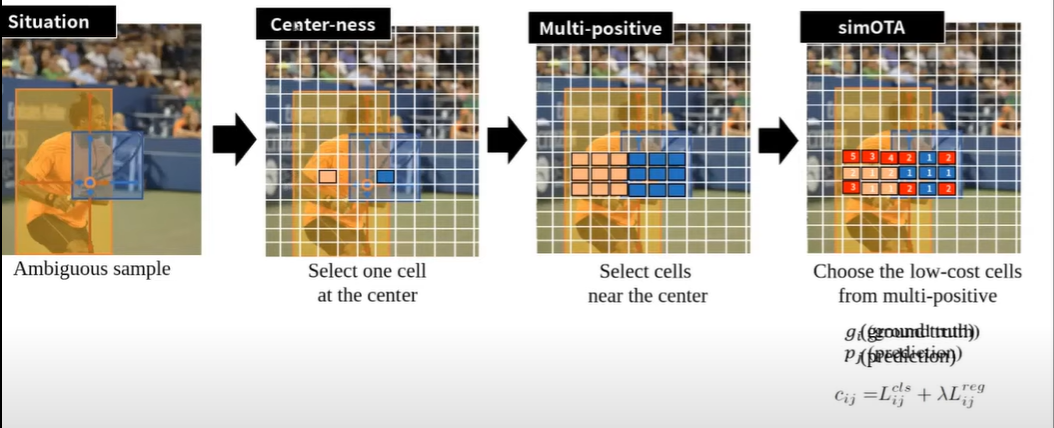
기본적인 Ancor free 방법만으로는 Anchor-based의 정확성을 따라잡기 힘듬에 따라 여러 방법들을 적용하게 됨
1. Center-ness ( FCOS 논문에서 처음 제안)
  - 위의 사진과 같이 동그라미 점의 cell이 prediction하고자 하는 cell이라면 오브젝트 레이블이 좀 불분명한 점이 있습니다. 이러한 문제 때문에 detection ratio가 떨어진다고 생각해서 FCOS 저자는 positive한 셀들중에서 오브젝트의 중심에 해당하는 셀들만 positive로 할당하는  Center-ness 방법을 사용해서 정확도를 좀 더 항샹 시킴
2. Multi-positive
   - 중앙에 있는 셀 말고도 그 주위에서도 좋은 prediction을 할 수 있는 셀들을 사용하는 방법. 센터 말고 주위의 셀들도 prediction하는 방법
3. simOTA
   - 각 cell의 loss를 구해서, 각 Cell에서 Loss가 조금 낮은 애들만 top k를 뽑아서 학습시키는 방법. 예를 들어 그림에서처럼 사람 cell에 해당하는 9개의 sample중에서 5개는 loss가 낮은데 이 낮은 친구들을 positive sample로 사용하자는 의미. 라켓에 해당하는 cell의 경우도 파란색으로 5개가 loss가 낮음 이 친구들을 positive sample로 사용하자!!

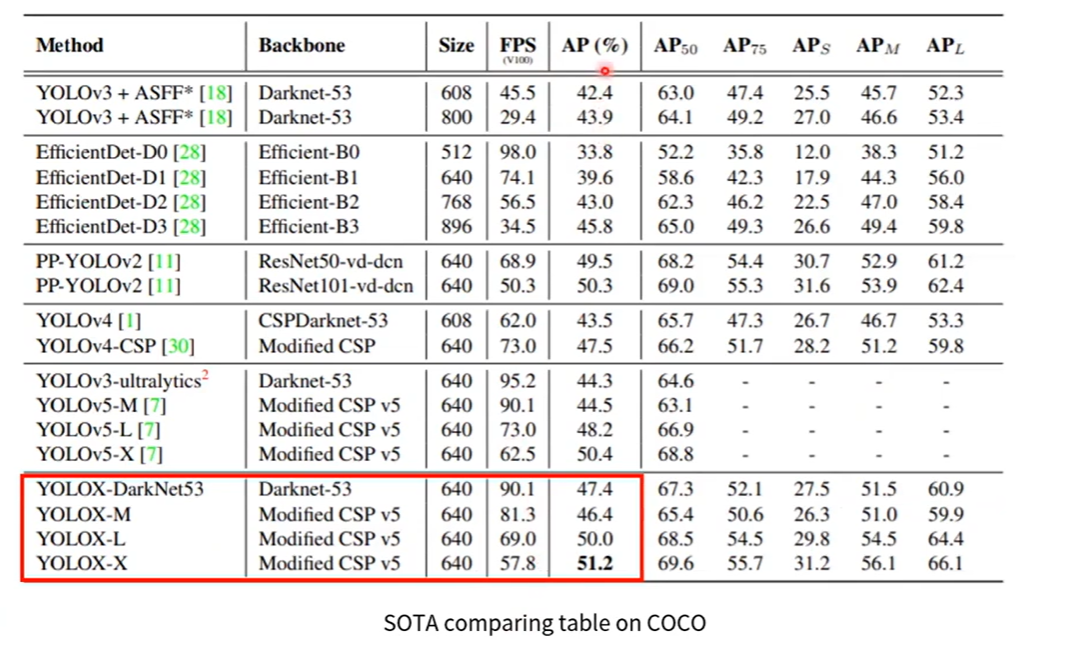
4. Experimental results

5. Conclusion

• 이 논문에서 anchor-free detector를 사용하여 YOLO 시리즈의 업데이트 버전을 제안
• 최근 고도화된 detection 기술인 decoupled head, advanced label assigning strategy등을 사용해 속도와 정확성이 전반적으로 훌륭한 성능을 보임
• 전반적으로 널리 쓰이는 YOLOv3의 아키텍쳐를 사용해서 AP(COCO)를 SOTA 최고로 개선시킴

Pose Estimation

• 주어진 영상 속 Human Object의 자세(pose)를 추정하는 것
• 해당 과제는 아래와 같이 불리기도 함
  • Key-point detection, Pose recognition
    • Key-points : 사람의 자세를 구성하는 주요 관절 포인트 지칭
• pose estimation : 특정 Pose를 만들어내는 Key-points들을 찾아내는 tast (= "Key-points Localiztion")

• Task (Single Person)

1. HPE(Human Pose Estimation )Task의 경우 크게 2D, 3D로 나누어 집니다. ( 여기서는 2D만 다루도록 하겠습니다.)
2. 2D를 크게 Single Person과 Multi Person으로 나눌 수 있습니다.
3. 신체의 머리, 어깨 등의 keypoint를 예측하는 방법으로 Direct Regression 그리고 HeatMap Regression으로 나눌 수 있습니다.

Direct Regression : 2차원 이미지 픽셀 값을 입력으로 이용하여 바로 좌표를 추정하는 방법으로 빠른 학습이 가능합니다. 하지만 사람이 복수로 존재하는 경우 적용하기 어렵고 키포인트 위치가 매우 비선형적이고 적합하게 매핑하기 어렵다는 것이 한계점을 가지고 있습니다.

HeatMap Regression : 신체 부위 중 키포인트가 존재할만한 위치를 확률적으로 HeatMap를 계산하고 HeatMap을 기반으로 키포인트 위치를 추정하는 방법입니다. 보다 시각적으로 직관적이고 동시에 사람이 다수일 경우도 적용이 가능하다고 합니다. ( 대부분 HeatMap 베이스로 예측하는 것이 성능이 훨씬 좋다고 알려져 있습니다.) 따라서 논문 마지막 부분에서도 Heatmap 방식을 적용했다고 합니다.

• Task (Multi Person)

1. Multi Person은 Top-down과 Bottom-up 방식으로 나누어 집니다.

• Top-down
  • Top-down 방식은 먼저 사람을 찾고 그 각각의 사람을 대상으로 키포인트 디텍션을 진행하게 됩니다.
  • 왼쪽부터 오른쪽 순서대로 바운딩 박스로 각각의 사람을 디텍션 하게 되고 그 뒤에 바운딩 박스 내에 있는 사람의 키포인트를 찾는 방식
  • 바텀업 방법에 비해 속도가 느리지만 정확도가 높음

• Bottom-up
  
  • Top-down 방식과 반대로 먼저 모든 키포인트들을 찾은 뒤에 그 각각의 키포인트들을 이어서 각 사람에 맞게끔 연결하는 방법
  • 일반적으로 바텀업 방법이 속도가 빠르지만 정확도가 떨어짐

HR-Net에 본격적으로 들어가기 전에 이전 방법들에 대해서 간단하게 설명하도록 하겠습니다.

위의 그림을 보게 되면 대부분 기존 방법들은 이미지를 고해상도에서 저해상도로 압축을 하고 저해상도에서 고해상도로 복원하는 과정을 거칩니다. 그리고 키포인트를 마지막 고해상도에서 찾습니다. 이러한 방법들을 이 논문에서는 직렬적인 시퀀셜한 구조라고 표현합니다.
왼쪽의 모델은 Stacked hourglass 모델로 symmetric하게 high-to-low에서 low-to-high로 진행되는 것을 볼 수 있으며 down sampleing 되기 전에 skip connection이 연결되어 feature 값이 전달되고 있음을 알 수 있습니다.
오른쪽의 모델 Simple Baseline의 경우 Strided Convolution으로 압축을 하고 Upsampling을 하는 과정에서 Transposed Convilution을 적용하게 됩니다.
이러한 직렬적인 구조는 압축하는 과정에서 지엽적인 정보들의 손실을 가져오게 되고 모든 프로세스가 upsampling에 의존하고 있다는 한계점이 있습니다.

HR Net도 위에 방법들과 기본적으로는 비슷하다. 근본적으로는 scale에 변화를 주면서 다양한 resolution에서 정보를 추출한다. 그럼에도 불구하고 다른 모델들보다 성능이 좋은 이유와 차별성에는 2가지가 있다.

1. High-to-low resolution을 Serially(X) Parallel(O)하게 적용한다. 이게 무슨 의미인지는 아래에 나와있다.

      기존 : Input받은 strand가 downsample 됨.

       HR : Input 받은 strand의 해상도는 쭉 유지가 되고 거기서 평행하게 downsample되는 strand가 분리된다.

이렇게 되면 최종적으로 predicted된 heatmap에 한번도 downsample/upsample되지 않은 input해상도 feature map이 영향을 주기 때문에 훨씬 정확하다.

2. Repeats multi-scale fusions

      기존 : 존재하는 대부분의 기법은 low-level and high-level representation을 더한다.

       HR : parallel한 sub-network간에 계속 정보를 주고 받는다. (그림을 보면 쉽게 알 수 있음)

같은 depth와 유사한 level의 low-resolution representation을 보조로 사용한다. predicted heatmap도 더 정확한 결과를 보인다.

결과적으로 HRNet의 경우 다양한 해상도의 subNet을 병렬적으로 유지함과 동시에 exchange unit을 통해서 전체적인 맥락과 국소적인 정보를 지속해서 교환하는 특성이 있다.

​

Parallel multi-resolution subnetworks (HR)

• NsrNsr에서 앞자리는 stage, r은 downsample된 단계를 의미한다. \
• NsrNsr은 첫번째 subnetwork(N11N11)의 해상도의 12r−112r−1 
• high-resolution subnetwork을 처음 stage로 시작한다.
• high-to-low resolution subnetworks을 하나씩 추가한다.

Repeated multi-scale fusion

다양한 scale을 반복적으로 fusion하는 괴정에서 Exchage Unit이란게 사용된다.

Exchange Unit이란 병렬 subnetowrk간에 정보를 전달해주는 역할을 하는 유닛이다.

how Exchage unit aggregated info for high, medium and low resolutions

서로 다른 resulution의 정보를 합칠때는 적절하게 upsampling / downsampling이 필요하다. 

아래 그림은 stage 3를 여러 exchange block으로 나눈 그래프이다. CbsrCsrb는 r번째 resultion, sth stage, bth block의 convolution unit을 의미한다.

• CbsrCsrb에서 s,b를 무시하고 r만 남겨놓는다. (resolution에 따른 차이만 보겠다는 의미)
• Input response maps: {X1​,X2​,...,Xs​} (resolution 단계는 1~S)
• Output response maps: {Y1​,Y2​,...,Ys​} (resolutions and widths = input)
• Yk=∑si=1a(Xi,k)Yk=∑i=1sa(Xi,k)   Each output is an aggregation of the input maps
• Ys+1=a(Ys,s+1)Ys+1=a(Ys,s+1) → Last Exchange Unit

Heatmap Estimation

최종적으로 heatmap은 Last exchange unit Ys+1Ys+1으로부터 나온 high-resolution representations output 으로 regress한다.

Loss Function은 평균 제곱 오차 MSE를 사용한다. 여기에 사용되는 GT heatmap은 각 keypoint에 2D 가우시안 분포를 적용해서 구한다.

Network Instantiation

ResNet 사용, resolution이 반으로 줄어들때마다 channel은 2배로 증가시킴.

3. Experiments

• COCO dataset 사용
• Evaluation Metric : OKS

OKS = ∑iexp(−d2i/2s2k2i)δ(vi>0)∑iδ(vi>0)∑iexp(−di2/2s2ki2)δ(vi>0)∑iδ(vi>0)

RESULTS ON COCO

출처 :

https://www.youtube.com/watch?v=w39bjQxm1eg 

https://www.youtube.com/watch?v=GmANBttiHx4 

활성화 함수(activateion function) : 입력 신호의 총합을 출력 신호로 변환하는 함수. 변환된 신호를 다음 뉴런에 전달한다. 입력 신호의 총합이 활성화를 일으키는지를 정하는 역할을 한다.

 

a = b+w1x1+w2x2 #가중치가 달린 입력 신호와 편향의 총합
y=h(a) #a를 함수 h()에 넣어 y를 출력

3-2 활성화함수

시그모이드 함수 (sigmoid function)

 

신경망에서는 활성화 함수로 시그모이드 함수를 이용하여 신호를 변환하고 그 변환된 신호를 다음 뉴런에 전달한다.

• 시그모이드 함수 구현하기
  브로드캐스트 기능: 넘파이 배열과 스칼라값의 연산을 넘파이 배열의 원소 각각과 스칼라값의 연산으로 바꿔 수행한다.

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
  return 1/(1+np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
#브로드캐스트
#넘파이 배열과 스칼라값의 연산을 넘파이 배열의 원소 각각과 스칼라값의 연산으로 바꿔 수행

plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

계단함수 (step function)

def step_function(x):
  return np.array(x>0, dtype=np.int)
  ##numpy 배열을 인수로 넣을 수 있게 하는 방법
    #x = np.array([-1.0, 1.0, 2.0])
    #y = x>0
    #y를 출력하면 0보다 큰 x값은 True로, 0보다 작거나 같은 값은 False로 나온다.
    #booleaan값을 int형으로 변환시키면 True는 0, False는 1이다.
        
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) 
plt.show()

 

 

ReLU함수 (rectified linear unit)

def relu(x):
  return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y= relu(x)
plt.plot(x, y)
plt.show()

3-3 다차원 배열의 계산

np.ndim(): 배열의 차원 수 확인
배열.shape: 배열의 형상 확인

import numpy as np

#1차원 배열
A = np.array([1,2,3,4])
np.ndim(A)
A.shape #튜플로 반환

#2차원 배열
B = np.array([[1,2], [3,4], [5,6]])
np.ndim(B)
B.shape
'''
[[1 2]
 [3 4]
 [5 6]]
2
(3, 2)
'''

행렬의 곱

 

#위 그림을 파이썬으로 구현
A = np.array([[1,2], [3,4]]) #2*2행렬
B = np.array([[5,6], [7,8]]) #2*2행렬
np.dot(A, B)
'''
(2, 2)
(2, 2)
array([[19, 22],
       [43, 50]])
'''​

신경망에서의 행렬 곱

X = np.array([1,2])
X.shape #(2,)

W = np.array([[1,3,5], [2,4,6]])
print(W)
'''
[[1 3 5]
 [2 4 6]]
'''
W.shape #(2,3)

Y = np.dot(X, W)
print(Y)
print(Y.shape)
'''
[ 5 11 17]
(3,)
'''

3층 신경망 구현하기

 

 

은닉층에서의 가중치 합(가중 신호와 편향의 총합)을 a로 표기하고 활성화 함수 h( )로 변환된 신호를 z로 표현한다.

 

1층의 '가중치 부분'을 행렬식으로 간소화하면

def init_network():
  network = {}
  network['w1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
  network['b1'] = np.array([0.1, 0.2, 0.3])

  network['w2'] = np.array([[0.1, 0.4], [0.2, 0.5],[0.3, 0.6]])
  network['b2'] = np.array([0.1, 0.2])

  network['w3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
  network['b3'] = np.array([0.1, 0.2])
  return network

def forward(network, x):
  w1, w2, w3 = network['w1'], network['w2'], network['w3']
  b1, b2, b3 = network['b1'], network['b2'], network['b3']

  a1 = np.dot(x,w1) + b1
  z1 = sigmoid(a1)
  a2 = np.dot(z1, w2) + b2
  z2 = sigmoid(a2)
  a3 = np.dot(z2, w3) + b3
  z3 = sigmoid(a3)
  return z3
  
network = init_network()

x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [0.57855079 0.66736228]

3-4. 출력층 설계하기

기계학습 문제는 분류(classification)와 회귀(regression)로 나뉜다.
일반적으로 회귀에는 항등함수를 분류에는 소프트맥스 함수를 출력층의 활성화 함수로 사용한다.

항등 함수와 소프트맥스 함수 구현하기

• 항등함수(identity function): 입력을 그대로 출력

• 소프트맥스 함수(softmax function):

def softmax(a):
  exp_a = np.exp(a)
  sum_exp_a = np.sum(exp_a)
  y = exp_a / sum_exp_a
  
  return y

a = np.array([0.3, 2.9, 4.0])
print(softmax(a)) # [0.01821127 0.24519181 0.73659691]

소프트맥스 함수 구현 시 주의점

지수함수를 사용하는 소프트맥스 함수는 '오버플로'의 문제가 발생해 수치가 '불안정'해질 수 있는 문제점이 있다.

• 오버플로(overflow) : 표현할 수 있는 수의 범위가 한정되어 너무 큰값은 표현할 수 없다.
• 소프트맥스 함수 구현 개선

def softmax(a):
  c = np.max(a)
  exp_a = np.exp(a-c) # 오버플로우 대책
  sum_exp_a = np.sum(exp_a)
  y = exp_a / sum_exp_a
  
  return y​

소프트맥스 함수의 특징

• 출력값은 0에서 1.0 사이의 실수이다.
• 출력의 총합은 1이다. -> 확률로 해석가능 (엄밀히 말하자면 확률은 아님, score라고 말하기도 한다.)
• 지수함수가 단조 증가 함수 이기 때문에 소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않는다. 결과적으로 신경망으로 분류할 때는 출력층의 소프트맥스 함수를 생략해도 된다.
  • • • • • • • • • • • • • • • •  

2-1. 퍼셉트론(Perceptron)

퍼셉트론(perceptron)은 프랑크 로젠블라트(Fank Rosenblatt)가 1957년에 고안안 알고리즘이다. 이 퍼셉트론

퍼셉트론(perceptron)은 프랑크 로젠블라트(Fank Rosenblatt)가 1957년에 고안한 알고리즘이다. 이 퍼셉트론이 바로 신경망(딥러닝)의 기원이 되는 알고리즘이다.

퍼셉트론은 다수의 신호(흐름이 있는)를 입력으로 받아 하나의 신호를 출력한다. 퍼셉트론은 이 신호를 입력으로 받아 '흐른다/안 흐른다'(1 또는 0)이라는 정보를 앞으로 전달한다.

 

 

위의 그림에서,

• x_1​과 x_2 ​는 입력 신호, y​는 출력 신호, w_1​과 w_2​는 가중치(weight)를 의미한다.
• 원을 뉴런 또는 노드라고 부른다.
• 입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다(w_1x_1,w_2,x_2​).
• 뉴런에서 전달 받은 신호의 총합이 임계값 θ를 넘을 때만 1을 출력

 

2-2. 단순한 논리 회로

A. AND 게이트

위의 표는 AND게이트의 진리표이며 이 AND게이트를 퍼셉트론으로 표현해보자. 이를 위해서는 ​ w_1, w_2, θ 의 값을 적절하게 정해야 한다.

예를 들어 , (w_1, w_2, θ) = (0.5, 0.5, 0.7) 일 때, AND 게이트의 조건을 만족한다.

B. NAND 게이트와 OR 게이트

NAND 게이트는 Not AND를 의미하며 AND 게이트의 출력을 반대로한 것과 같다.

OR 게이트는 입력 신호 중 하나 이상이 1이면 출력이 1이 되는 논리 회로다.

C. XOR 게이트

XOR 게이트는 베타적 논리합 이라는 논리 회로다.

 

그림 8에서 보이는 것과 같이 기존의 게이트에서 보이지 않던 비선형적인 성질이 보인다. 따라서 하나의 게이트로 구현할 수 없어서 기존의 게이트를 조합하는 형식으로 구현하였다.