0. Abstarct
(0-1) Residual Learning Framework 제안
- 특징 1 : 기존 Neural Network(ex : VGG)보다 Layer 수가 더 많아도 학습(train) 및 최적화(optimize)가 쉬움
- * 학습 및 최적화가 쉽다 = Loss 값이 쉽게 떨어진다 = 최적의 딥러닝 모델 파라미터를 찾기 쉽다
- 특징 2 : Residual Learning Framework의 깊이가 깊어져도(=Layer 수가 더 많아져도), 정확도가 꾸준하게 향상됨
- * 정확도 : 이미지 내 클래스 분류 정확도 등등...
- 특징 3 : 기존 Neural Network보다 더 많은 Layer 수를 가져도, 파라미터 수는 더 적음
- * ResNet-152(layers)는 VGG-19보다 Layer 수는 8배 더 많으나, 더 적은 모델 파라미터 수(lower complexity)를 가짐
1. Introduction
(1-1) 네트워크의 깊이는 성능에 중요한 영향을 끼침
- Deep Neural Network는 low/mid/high level features를 통합하고, 여러 개의 Layer에서 end-to-end 방식으로 class를 분류함

- 이때 feature의 level은 stacked layers 갯수(= Depth)에 영향을 받음
- -> Neural Network의 Layer 수가 많아질수록 근사화(Approximation)가 강력해짐
- * 본문에서는 근사화를 Identity Mapping 표현으로 대체
- 최근 연구(본문의 참고 문헌 : 41, 44)에 따르면 Neural Network의 Depth는 성능(정확도) 향상에 영향을 줌
(1-2) 네트워크의 깊이가 깊어지면 발생하는 문제 : Gradient Vanishing/Exploding (소멸/발산)
- Gradient Vanishing, Exploding 문제의 정의는 아래와 같음

- 그러나! 이러한 문제는 normalized initialization, iintermediate normalization layers, SGD 등을 통해 대부분 해결됨
(1-3) 그럼에도 해결되지 않은 문제 : Degradation (성능 저하)- Degradation 문제 : Neural Network의 깊이가 증가할수록, 정확도는 포화되다가 급격하게 정확도 감소
- -> Layer 수를 증가시키는 것은 딥러닝 모델에 높은 학습 에러값을 발생
- 이러한 저하 문제는 오버피팅에 의해 발생되는 것이 아니며, 최적화가 쉽지 않다는 것을 보여줌
- 단순하게 Layer 수를 증가하는 것은 성능 향상을 위한 해결책이 아님

- Neural Networks는 Layer의 깊이(Depth)가 깊어질수록 error가 증가하고, 그림 1에서 그 현상을 볼 수 있음
- 왼쪽 그림 1 : CIFAR-10 데이터에 대한 Tranning Error
- 오른쪽 그림 1 : CIFAR-10 데이터에 대한 Test Error
- 빨간색 그래프 : 56-layer (비교적 깊이가 깊은 네트워크)
- 노란색 그래프 : 20-layer (비교적 깊이가 얕은 네트워크)
- * 번외 : iter과 epoch의 차이

iter과 epoch의 차이
(1-4) 본문의 핵심 아이디어- 핵심 아이디어 : Deep Residual Learing Framework를 소개함으로써 degradation 문제를 해결

그림 2. 기존 Neural Network's Block VS Residual Network's Block
- Underlying Mapping (기존 매핑) : 기존 Neural Network의 Output -> H(x)
- Residual Mapping (잔차 매핑) : H(x) = F(x) + x // x : Layer's input
- 본 연구의 가정 : residual mapping이 unreferenced mapping보다 최적화하기 쉬움
(1-5) Residual Mapping의 구현 : Short Connections- residual mapping(=F(x) + x)은 short connection에 의해 구현 가능
- 그림 2의 오른쪽(residual block)에서 'identity'에 해당하는 곡선이 short connection에 해당
- Short Connection의 역할 : Layer를 하나 혹은 그 이상을 skip & identity mapping 수행
- * short connection에 layer 추가가 대신 identity short connection(layer의 입력을 그대로 출력부에 전송)을 사용하면, 추가적인 파라미터 수 혹은 computational complexity에 영향을 거의 주지 않음
(1-6) 본문의 기여점- (1) Layer 수가 많아져도 최적화하기 쉬운 Deep Residual Learning Framework 제안
- (2) Layer 수가 많아져도 정확도 향상이 보증됨
- (3) 특정한 데이터셋(ex : ImageNet) 뿐만 아니라 다양한 데이터셋(ex : CIFAR-10 등등)에서도 높은 성능을 보이며, 이는 범용적인 아이디어로 증명됨
- (4) 기존 Network보다 Layer 수가 많아도, 파라미터 수는 적음 (=Lower Complexity)
2. Related Work- * 해당 파트는 제가 전통 컴공생이 아닌 관계로... 깊숙하게 들어가지는 않고, 대략적인 흐름만 케치해보겠습니다!
- 기존 image recognition에서 VLAD, Fisher Vector 개념이 등장

- 이 개념을 적용하기 위해 편미분 방정식(PDE : Partial Differential Equations)을 풀어야함 (이미지는 2차원이니깐!)
- 이 편미분 방정식을 풀기위해 residual 기법이 적용됐으며, 이는 기존의 풀이보다 최적화가 간단해짐
2-2. Shortcut Connections- 기존의 gradient vanishing/exploding 문제를 해결하기 위해 몇몇 중간의 layer를 최종 layer(classifiers)에 연결함으로써 성능 향상을 시도
- 본문과 비슷한 연구 주제로 "Highway networks // 참고문헌 42, 43"이 있으나, layer 깊이에 따른 성능 향상에 대한 지표를 제시하지 않음
3. Residual Learning- 이 절의 내용은 (1-3), (1-4) 내용과 유사합니다.
- 내용 요약 : 단순하게 Layer를 쌓는 형태는 identity mapping에 적합하지 않으므로(=Degradation 문제 발생), Residual Mapping을 통해 Degradation 문제를 해결할 것이다!
3-2. Identity Mapping by shortcuts- Residual Block을 다음과 같이 정의



- x, y : Layer의 input, output
- F(x, {W_i}) : Residual Mapping
- W_1, W_2 : 첫, 두번째 layer의 가중치(=모델 파라미터)
- σ : ReLU (Activation Function)
- * Bias(편향)은 수식의 간략화를 위해 생략
3-2.-(2) Shortcut Connection- F + x : shortcut connection에 의해 구현 가능
- F와 x의 차원이 다르므로, 차원을 맞춰줘서 element-wise addition(단순한 행렬 합)을 진행해야 함
- 본문에서는 1*1 conv layer를 활용하여 Layer의 중간 output인 F와 차원을 맞춰줌

- 번외 : Residual Block의 Layer 수를 2개, 3개 혹은 그 이상으로 해도 상관 없으나, Layer 수를 1개만 했을 때는 효과가 거의 없었음

3-3. Network Architectures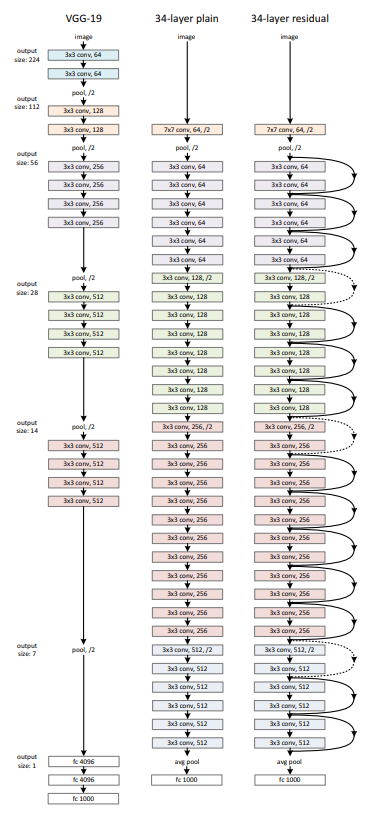
- VGG-19 아키텍쳐에 영감을 받음 & 3*3 conv filter 사용
- VGG와의 차이점 1 : Max Pooling 대신 Conv layer에서 Stride 2를 사용하여 Feature Map의 size를 절반으로 감소
- VGG와의 차이점 2 : Feature Map의 size가 절반으로 감소하면, 필터의 수는 2배로 증가시켜서, 레이어마다의 time complexity를 보존
- VGG와의 차이점 3 : 위의 테크닉을 적용하여, VGG보다 레이어 수는 15개 더 많지만, 파라미터 수는 VGG19의 18%에 해당
(2) Residual Network- Plain Network에 Shortcut Connection을 적용

- Identity Shortcuts은 input과 output이 동일한 차원일때 사용 가능
- 차원의 증가하면, 2가지 옵션을 선택할 수 있음
- (옵션 1) : 차원 증가를 위해 zero padding 적용 -> identity shortcuts 효과
- (옵션 2) : 차원 증가를 위해 projection shortcut 적용 -> 1*1 conv를 활용
3-4. Implementation- 데이터 증강을 위해 학습 데이터는 256~480 pixel 중 랜덤하게 resize된 후, 224*224 crop 적용
- 혹은 horiziontal flip 적용

horiziontal flip
- 데이터 전처리를 위해 pixel mean subtracted 적용
- 각 Conv layer와 activation function 사이에 Batch Normalization 적용
- mini-batch 256으로 SGD 최적화 사요
- 학습률은 0.1로 시작하다가, error가 감소되지 않으면 10으로 나눔
- 학습 횟수 : 60*10^4 iter
- weight decay : 0.0001
- momentum : 0.9
- No Dropout
- 테스트 방법 : standard 10-crop testing 적용

10 crop test
- multiple scales(224, 256, 384, 480, 640)에서 평균 점수를 사용
4. Experiments(1) ImageNet Dataset- ResNet을 ImageNet 2012 classification dataset에서 top-1, top-5 error rate에 대해 평가(evaluate) 진행
- * top-1, top-5 error에 대한 깔끔하게 정리된 설명이 얼마 없어서... accuracy로 대체합니다~

top-1, top-5 accuracy의 정의
- class 개수 : 1,000개
- 학습 데이터 수 : 128만개 (1.28 million)
- 검증 데이터 수 : 5만개 (50k)
- 테스트 데이터 수 : 10만개 (100k)
(2) Architectures for ImageNet
- ResNet 아키텍쳐 : conv 3_1, conv 4_1, conv 5_1에서 다운 샘플링 (with stride 2)

그림 5. Basic Block(좌) VS Bottleneck Block(우)
- Basic Block (그림 5의 왼쪽) : 한 블록에 stacked된 layer 2개 -> ResNet 18/34
- Bottleneck Block (그림 5의 오른쪽) : 한 블록에 stacked된 layer 3개 -> ResNet 50/101/152
(3-1) Plain Network for ImageNet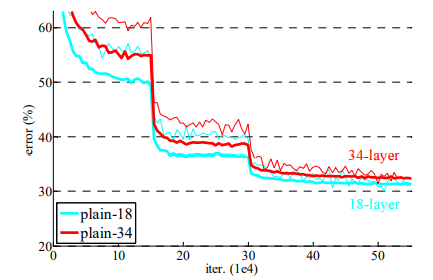
그림 4. ImageNet 데이터에 대한 학습, 검증 에러 (Plain Net) 
표 2. ImageNet 검증 데이터에 대한 Top-1 error %
- 표 2를 보면, PlainNet은 더 깊은 34-layer가 더 얕은 18-layer보다 더 큰 validation error를 가지고 있는 것을 보여줌
- 그림 4에서도 plain-34가 plain-18보다 더 큰 train/val error를 가지고 있음을 보여줌
- * 그림 4에서 굵은 선이 val error, 얇은 선이 train error
- 결론 : plain에서는 degradation 문제가 관찰됨
- 가설 1 : Gradient Vanishing에 의해 Degradation 발생
- 가설 1에 대한 반박 1 : PlainNet은 Batch Normalization에 의해 학습되어, forward propagation은 0이 아닌 분산을 가짐
- 가설 1에 대한 반박 2 : Backward Propagated Gradients는 BN과 함께 healty norms으로 보임
- 결론 1 : forward 혹은 backward 신호(값)은 소멸(vanish)되지 않음!! -> Gradient Vanishing은 Degradation의 원인이 아님
- 정확한 원인은 추후에 연구될 예정...
- * Batch Normalization이란? : https://sacko.tistory.com/44
문과생도 이해하는 딥러닝 (10) - 배치 정규화
2017/09/27 - 문과생도 이해하는 딥러닝 (1) - 퍼셉트론 Perceptron 2017/10/18 - 문과생도 이해하는 딥러닝 (2) - 신경망 Neural Network 2017/10/25 - 문과생도 이해하는 딥러닝 (3) - 오차 역전파, 경사하강..
sacko.tistory.com
(4-1) Residual Networks for ImageNet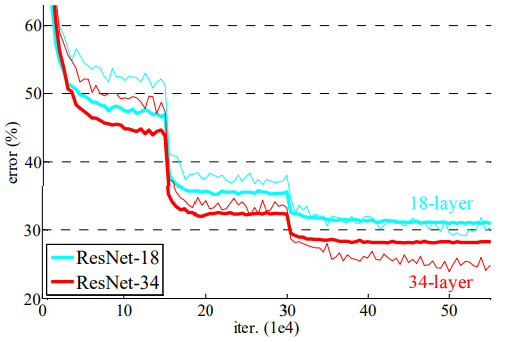

- 그림 4, 표 2에서 볼 수 있듯이, ResNet-34는 ResNet-18보다 성능이 향상됨
- * Top-1 error 기준, 약 2.8% 향상
- 이는 ResNet이 Degradation 문제를 해결했으며, Depth가 증가해도 정확도가 향상된다는 점을 보여줌
- ResNet-34는 Plain-34보다 top-1 error가 약 3.5% 감소함 -> ResNet은 성공적으로 error를 줄일 수 있음
- 반면, ResNet-18과 plain-18은 정확도가 비슷하지만, 그림 4를 비교하면 수렴 속도는 ResNet-18이 더 빠름
* 제 눈에는 둘다 비슷비슷 해보이는데... 논문에선 그렇다고 하니깐... 넘어가봅시다 ㅋㅋ- 즉, ResNet은 초기에 빠르게 수렴함으로써 최적화를 용이하게 함
(5) Identity VS Projection Shortcuts
- Shortcut Connections에 3가지 옵션을 부여한 후, 성능을 비교
- 옵션 A :
- - 차원 증가를 위한 shorcut : zero-padding
- - 그 외 : identity (parameter-free, 단순히 layer의 input을 더함)
- 옵션 B :
- - 차원 증가를 위한 shortcut : projection shortcut
- - 그 외 : identity (parameter-free, 단순히 layer의 input을 더함)
- 옵션 C :
- - 모든 shortcut : projection shortcut

- 옵션 B의 성능이 옵션 A보다 살짝 높음 (top-1 error 기준, 약 0.5%)
- 이는 옵션 A의 zero-padding으로 추가된 차원이 실제로 residual learning이 없기 때문이라고 추측됨 (값이 0이기 때문)
- 옵션 C의 성능이 옵션 B보다 살짝 높음 (top-1 error 기준, 약 0.3%)
- 이는 projections shortcut에 의해 추가된 파라미터(W_s) 때문이라고 추측됨
- 옵션 A/B/C 간의 성능 차이가 작기 때문에, degradation 문제를 해결하기 위해 projection shortcuts이 필수적이 아니라는 것을 볼 수 있음
- 따라서 본문의 후반에서는 memory/time complexity와 모델 사이즈를 줄이기 위해, 옵션 C를 사용하지 않을 예정
(6) Deeper Bottleneck Architectures- Basic Block은 Layer가 50층 이상으로 깊어지면, 연산 효율이 좋지 않음
- 연산 효율을 좋게 하기 위해, bottleneck block을 새로 디자인함

- Bottleneck Block은 3개의 Layer를 쌓음 -> 1*1, 3*3, 1*1 convolution으로 구성
- Bottleneck Block은 Basic Block 보다 Layer 수가 1개 더 많지만, time complexity는 비슷함
- Bottleneck Block에는 옵션 B(차원 증가 shortcut : projection, 그 외 : identity)를 적용
- (4-2) Plain Networks VS Residual Networks for ImageNet
- (3-2) Plain Network에서 발생하는 Degradation의 원인 분석
- 4-1. ImageNet Classification
- <학습 관련 인자>
- 3-2.-(1) Residual Blcok
- 3-1. Residual Learning
- * 1x1 conv이 연산 효율이 좋은 이유 : https://hwiyong.tistory.com/45
1x1 convolution이란,
GoogLeNet 즉, 구글에서 발표한 Inception 계통의 Network에서는 1x1 Convolution을 통해 유의미하게 연산량을 줄였습니다. 그리고 이후 Xception, Squeeze, Mobile 등 다양한 모델에서도 연산량 감소를 위해 이..
hwiyong.tistory.com
4-2. CIFAR-10 and Analysis- class 수 : 10개
- 학습 데이터 수 : 5만개 (50k) -> 학습 45k, 검증 5k로 split
- 검증 데이터 수 : 1만개 (10k)
(2) ResNet Architecture For CIFAR-10- 네트워크 input : 32*32 pixel (pixel mean subtracted 전처리 적용)
- * 이미지 크기가 작기 때문에, 첫번째 레이어는 7*7 -> 3*3 conv layer로 변경
- 레이어 구성 : 6n + 2
- * 6n : 3*3 convolutions
- * 2 : Global average pooling layer & 10-way Fully-Connected Layer


- weight decay : 0.0001
- momentum : 0.9
- weight initialization 적용
- Batch Normalization 적용
- Dropout 미적용
- mini-batch size : 128
- GPU 2개 사용
- 학습률 : 0.1 -> 32k iter에서 0.01, 48k iter에서 0.001, 64k iter에서 학습 종료
- Data 증강 : 학습 데이터의 각 사이드에 4픽셀 씩 패딩 후, 랜덤하게 32*32 crop

- n = 3, 5, 7, 9, 18을 적용하여 20, 32, 44, 56, 110 layer를 생성
- * ex) n=3일 때, 6*n + 2 = 6*3 + 2 = 20 layer
- CIFAR-10 데이터에서도, plainNet은 layer 수가 증가함에 따라 error가 증가하는 것을 볼 수 있음
- * 점선 : train error, 굵은 실선 : test error
- * Plain-110 layer는 error가 60% 이상이여서, 비교 대상에서 제거
- 반면 ResNet은 Layer 수가 110개까지 증가해도, error가 감소하는 것을 볼 수 있음
- 즉 ResNet은 데이터셋 종류와 관계없이, 범용적인 알고리즘이라는 것을 증명
(3) Analysis of Layer Responses
- 그림 7은 layer responses의 표준 편차(std)를 보여줌 (after Batch Normalization, before activation function)
- * 표준 편차의 정의 : 분산의 제곱근 -> 표준 편차가 작을 수록 평균 값에서 데이터(변량)들의 거리가 가까움
- 결과 분석 1 : ResNet은 PlainNet보다 전반적으로 std가 작음
- 결과 분석 2 : 깊은 ResNet(56, 110)이 얕은 ResNet(20)보다 std가 작음
- 이러한 관찰로 봤을 때, ResNet은 PlainNet보다 최적화가 용이하고, Depth가 깊어져도 성능 향상이 보증됨
(4) Exploring Over 1000 Layers
- n=200으로 하면, 1202-layer가 생성됨
- * 위 그림 6 역시, 점선이 train error, 굵은 실선이 test error
- ResNet 110과 1202를 비교했을 때, train error은 거의 유사함
- 그러나 test error는 ResNet 110이 더 낮음
- ResNet 1202가 ResNet 110 보다 성능이 안좋은 이유는 overfitting이 원인이라고 추측됨
- 이러한 overfitting은 DropOut등을 통해 해결할 수 있음

DropOut
4-3. Object Detection on PASCAL and MS COCO
- Object Detection에서 Backbone으로 ResNet을 사용하면, 성능 향상 가능
- <결과 분석 1 : Depth에 따른 error 비교>
- <그 외 학습 인자>
- (1) CIFAR-10 Dataset
'논문' 카테고리의 다른 글
| YOLOX 논문리뷰 (0) | 2022.05.09 |
|---|---|
| Pose Estimation - HRNet 논문리뷰 (0) | 2022.05.02 |