
위의 그림 속 신경망은 3층으로 구성되어있지만 가중치를 갖는 층이 2개이기 때문에 2층 신경망 이라고 한다.

y=0 (b+w1x1+w2x2<=0)
y=1 (b+w1x1+w2x2>0)
편향(bias)은 하나의 뉴런으로 입력된 모든 값을 다 더한 다음에(가중합이라고 합니다) 이 값에 더 해주는 상수입니다. 이 값은 하나의 뉴런에서 활성화 함수를 거쳐 최종적으로 출력되는 값을 조절하는 역할을 함
활성화 함수(activateion function) : 입력 신호의 총합을 출력 신호로 변환하는 함수. 변환된 신호를 다음 뉴런에 전달한다. 입력 신호의 총합이 활성화를 일으키는지를 정하는 역할을 한다.

a = b+w1x1+w2x2 #가중치가 달린 입력 신호와 편향의 총합
y=h(a) #a를 함수 h()에 넣어 y를 출력
3-2 활성화함수
시그모이드 함수 (sigmoid function)

신경망에서는 활성화 함수로 시그모이드 함수를 이용하여 신호를 변환하고 그 변환된 신호를 다음 뉴런에 전달한다.
- 시그모이드 함수 구현하기
브로드캐스트 기능: 넘파이 배열과 스칼라값의 연산을 넘파이 배열의 원소 각각과 스칼라값의 연산으로 바꿔 수행한다.
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
#브로드캐스트
#넘파이 배열과 스칼라값의 연산을 넘파이 배열의 원소 각각과 스칼라값의 연산으로 바꿔 수행
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
계단함수 (step function)
def step_function(x):
return np.array(x>0, dtype=np.int)
##numpy 배열을 인수로 넣을 수 있게 하는 방법
#x = np.array([-1.0, 1.0, 2.0])
#y = x>0
#y를 출력하면 0보다 큰 x값은 True로, 0보다 작거나 같은 값은 False로 나온다.
#booleaan값을 int형으로 변환시키면 True는 0, False는 1이다.
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
ReLU함수 (rectified linear unit)

def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y= relu(x)
plt.plot(x, y)
plt.show()


3-3 다차원 배열의 계산
np.ndim(): 배열의 차원 수 확인
배열.shape: 배열의 형상 확인
import numpy as np
#1차원 배열
A = np.array([1,2,3,4])
np.ndim(A)
A.shape #튜플로 반환
#2차원 배열
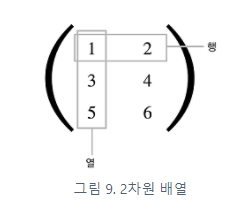
B = np.array([[1,2], [3,4], [5,6]])
np.ndim(B)
B.shape
'''
[[1 2]
[3 4]
[5 6]]
2
(3, 2)
'''
행렬의 곱

#위 그림을 파이썬으로 구현
A = np.array([[1,2], [3,4]]) #2*2행렬
B = np.array([[5,6], [7,8]]) #2*2행렬
np.dot(A, B)
'''
(2, 2)
(2, 2)
array([[19, 22],
[43, 50]])
'''
신경망에서의 행렬 곱

X = np.array([1,2])
X.shape #(2,)
W = np.array([[1,3,5], [2,4,6]])
print(W)
'''
[[1 3 5]
[2 4 6]]
'''
W.shape #(2,3)
Y = np.dot(X, W)
print(Y)
print(Y.shape)
'''
[ 5 11 17]
(3,)
'''
3층 신경망 구현하기


은닉층에서의 가중치 합(가중 신호와 편향의 총합)을 a로 표기하고 활성화 함수 h( )로 변환된 신호를 z로 표현한다.

1층의 '가중치 부분'을 행렬식으로 간소화하면

def init_network():
network = {}
network['w1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['w2'] = np.array([[0.1, 0.4], [0.2, 0.5],[0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['w3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
w1, w2, w3 = network['w1'], network['w2'], network['w3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x,w1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, w2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, w3) + b3
z3 = sigmoid(a3)
return z3
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [0.57855079 0.66736228]
3-4. 출력층 설계하기
기계학습 문제는 분류(classification)와 회귀(regression)로 나뉜다.
일반적으로 회귀에는 항등함수를 분류에는 소프트맥스 함수를 출력층의 활성화 함수로 사용한다.
항등 함수와 소프트맥스 함수 구현하기
- 항등함수(identity function): 입력을 그대로 출력

- 소프트맥스 함수(softmax function):

def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
a = np.array([0.3, 2.9, 4.0])
print(softmax(a)) # [0.01821127 0.24519181 0.73659691]
소프트맥스 함수 구현 시 주의점
지수함수를 사용하는 소프트맥스 함수는 '오버플로'의 문제가 발생해 수치가 '불안정'해질 수 있는 문제점이 있다.
- 오버플로(overflow) : 표현할 수 있는 수의 범위가 한정되어 너무 큰값은 표현할 수 없다.
- 소프트맥스 함수 구현 개선

-> 소프트맥스의 지수 함수를 계산할 때 어떤 정수를 더해도(혹은 빼도) 결과는 바뀌지 않는다.
-> C '에 어떤 값을 대입해도 상관없지만 오버플로를 막기 위해 입력 신호 중 최댓값을 이용하는 것이 일반적이다.
def softmax(a):
c = np.max(a)
exp_a = np.exp(a-c) # 오버플로우 대책
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
소프트맥스 함수의 특징
- 출력값은 0에서 1.0 사이의 실수이다.
- 출력의 총합은 1이다. -> 확률로 해석가능 (엄밀히 말하자면 확률은 아님, score라고 말하기도 한다.)
- 지수함수가 단조 증가 함수 이기 때문에 소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않는다. 결과적으로 신경망으로 분류할 때는 출력층의 소프트맥스 함수를 생략해도 된다.
-
'vison_study' 카테고리의 다른 글
| 2.1 퍼셉트론 (밑바닥부터 딥러닝) (0) | 2021.12.22 |
|---|---|
| Torch tensor to numpy(in use Opencv) (0) | 2021.06.28 |
| Vison Study #2 (0) | 2021.06.27 |
| Vison_study #1 (0) | 2021.06.27 |